
Boolean Algebra
Boolean algebra plays a key role in computer science, advanced mathematics, physics, digital logic, set theory, statistics, etc. The term Boolean algebra is also known as binary algebra or logical algebra. It signifies the core concept of modern computing. The term Boolean algebra was introduced in the 19th century by George Boole.
Boolean algebra remains important as a fundamental pillar in developing digital electronics and all modern programming languages. In this article, we will elaborate on the concept of Boolean algebra, its definition, important types, and significant applications.
Defining Boolean Algebra
Boolean algebra is a branch that deals with variables that can take on one of two possible values: true or false, often represented by 1 and 0, respectively.
Since its introduction, Boolean Algebra has become the foundation for all arithmetic and logical operations performed by computers.
In Boolean Algebra, the basic operations are defined on these binary values ( 0 and 1). The primary operations include:
- AND Operation
- OR Operation
- NOT Operation
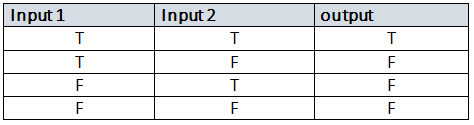
AND Operation:
Denoted by a dot (·) or sometimes omitted, this operation results in true (1) only when both of its operands are true; otherwise, it results in false (0).
Example: 1⋅1=11⋅1=1, 1⋅0=01⋅0=0, 0⋅1=00⋅1=0, 0⋅0=00⋅0=0
In the truth table ‘0’ represents the ‘false’ and ‘1’ represents the ‘true’.
Truth Table :
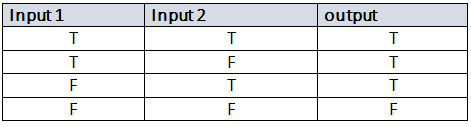
OR Operation :
Denoted by a plus sign (+) or sometimes a wedge (∨), this operation results in true if at least one of its operands is true.
Example: 1+1=11+1=1, 1+0=11+0=1, 0+1=10+1=1, 0+0=00+0=0
Truth Table:
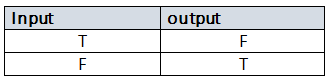
NOT Operation:
Denoted by a bar over the variable or the symbol ¬, this operation negates the input, turning true into false and false into true.
Example: ¬1=0¬1=0, ¬0=1¬0=1
Truth Table:
Boolean Algebra has applications in various fields, especially in computer science and digital electronics, where it is used to design and analyze digital circuits and systems.
Laws & Theorems of Boolean Algebra
Boolean Algebra, developed by mathematician George Boole, consists of several laws and theorems that form the basis for logical operations in digital circuits and computer science. These laws help simplify and analyze complex logical expressions. Here are some fundamental laws and theorems of Boolean Algebra:
Identity Laws:
- Identity Law for OR: A + 0 = A
- Identity Law for AND: A * 1 = A
Domination Laws:
- Domination Law for OR: A + 1 = 1
- Domination Law for AND: A * 0 = 0
Complement Laws:
- Complement Law for OR: A + A’ = 1
- Complement Law for AND: A * A’ = 0
Idempotent Laws:
- Idempotent Law for OR: A + A = A
- Idempotent Law for AND: A * A = A
- Double Negation Law: A = A
Commutative Laws:
- Commutative Law for OR: A + B = B + A
- Commutative Law for AND: A * B = B * A
Associative Laws:
- Associative Law for OR: (A + B) + C = A + (B + C)
- Associative Law for AND: (A * B) * C = A * (B * C)
Distributive Laws:
- Distributive Law for OR over AND: A + (B * C) = (A + B) * (A + C)
- Distributive Law for AND over OR: A * (B + C) = (A * B) + (A * C)
Absorption Laws:
- Absorption Law for OR: A + (A * B) = A
- Absorption Law for AND: A * (A + B) = A
De Morgan’s Laws:
- De Morgan’s Law for OR: (A + B)’ = A’ * B’
- De Morgan’s Law for AND: (A * B)’ = A’ + B’
- Redundancy Law: A + A’ * B = A + B
Theorem of Null Elements:
- A + A’ = 1
- A * A’ = 0
Theorem of double complement:
∼(∼A) = A or A’’ or A = A
Understanding these laws and theorems of Boolean Algebra is crucial for designing and analyzing digital circuits and logical expressions. They provide a foundation for creating efficient and optimized logical structures in various applications.
Also, you can simplify Boolean algebra problems by using truth tables, Boolean laws, or Boolean expression simplifier.
Related :
